Expected Death Analysis

Covid-19 is causing a higher death rate than normal. There has been some controversy as to whether covid-19 was the cause of death, even if it was present in the deceased. To avoid this controversy, it's possible to just look at the number of deaths in a particular week and compare it with the number the same week over the past few years. (See, for example, Mortality surveillance during the COVID-19 pandemic in the Bulletin of the World Health Organization, New York Times A Positive Covid Milestone. ) The graph below uses data from the CDC ( JSON). In particular, the week of reported deaths and the percentage of expected deaths fields are used. The percent of expected deaths compares the death count in the particular week to the average for that week in 2017 throgh 2019. Comparing to same week data for previous years removes seasonal effects on death rates.

There is also an interesting analysis in the New York Times. The NYT analysis shows the consistently improving death rate (deaths per 100,000 population) until 2020. Analysis of death rates is interesting since there are so many variables. The number of deaths per 100,000 population is considerably less than half of what it was in 1920, probably due to medical advances. Other effects on the death rate include the age of the population, the expected lifespan of the population, and many other effects. The NYT article also has a chart comparing the death rate to the previous year showing a substantial increase in 2020.

As can be seen in the raw CDC data through March 14, 2020, this number is pretty stable. However, after March 14, we see the percentage of expected deaths increase dramatically. Towards the end of the dataset, the percentage of expected deaths is very low. This is because the CDC records the actual date of the death, but may not receive that report for several weeks. We can make predictions based on early reports (see below).

Causes of an increase in the number of deaths include an increase in disease caused deaths, an increase in population, and an aging population. Because the below graph based on CDC data compares deaths each week to the average for that week in the years 2017 through 2019, we expect an increase due to population increase and an aging population.

Using total US population data from here, we find the percentage population increase for years 2020 through 2022 compared to the average population in the years 2017 through 2019.

Year	US Population
2017	329,791,231
2018	332,140,037
2019	334,319,671
Average	332,083,600

Comparing the population in successive years to the average for 2017 through 2019, we get the table below.

Year	US Population	Increase Over 2017-2019
2020	335,942,003	3,858,403	1.2%
2021	336,997,624	4,914,024	1.5%
2022	338,289,857	6,206,257	1.9%
2023	339,996,563	7,912,963	2.4%

We expect a minor increase (less than 2.5%) in the number of deaths compared to those in 2017 through 2019 due to US population increase.

Due to the "baby boom" following World War 2, we expect an increase in the number of deaths from an aging population. According to CDC data , the average lifespan at birth for people born in 1950 was 68.2 years. CDC data shows US births for each year. The table below shows the number of people expected to die in recent years based on an expected lifespan of 68 years.

Year of Expected Death	Birth Year	Births, Expected Deaths
2017	1949	3,649,000
2018	1950	3,632,000
2019	1951	3,820,000
2020	1952	3,909,000
2021	1953	3,959,000
2022	1954	4,071,000
2023	1955	4,097,000
2024	1956	4,210,000
2025	1957	4,300,000

Averaging the number of deaths expected in 2017 through 2019 based on births in 1949 through 1951, we get 3,700,333 expected deaths. Due to the increased birth rates continuing from 1952, we expect increased deaths from 2020 through 2023 as shown below. Expected Deaths in the table below is based on the number of births 68 years earlier.

Year	Expected Deaths	Excess of 2017-2019 Expected Deaths
2020	3,909,000	208,667	5.6%
2021	3,959,000	258,667	7.0%
2022	4,071,000	370,667	10.0%
2023	4,097,000	396,667	10.7%
2024	4,210,000	509,667	13.8%
2025	4,300,000	599,667	16.2%

As suggested above, we expect an increase in the number of deaths due to an increasing population, an aging population, and disease. The table below summarizes the percentage increase in deaths over that in the years 2017 through 2019 due to population increase and an aging population (increased deaths due to increased births 68 years earlier).

	Increase Over 2017-2019 Due To
Year	Population Increase	Aging Popluation
2020	1.2%	5.6%
2021	1.5%	7.0%
2022	1.9%	10.0%
2023	2.4%	10.7%

In the year 2020, based on the table above, we expect about a 6.8% increase in deaths over 2017 through 2019 due to population increase and population aging. The graph below shows that in that year the increase in deaths substantially increased above this number, peaking at 43% over the expected deaths during the week of April 10. Looking at the year 2023, we expect about a 13.1% increase in deaths over 2017 through 2019 due to population increase and population aging. Though a bit early to tell at this writing (March 2023), it appears the excess death rate (over 2017-2019) is running in this area. As such, the contribution due to unusual disease such as covid 19 may be over. Not considered in this analysis, however, would be a decrease in future deaths due to deaths occuring earlier than expected (you only die once).

According to this document at medium.com, the timeline for infections ending in death averages as below:

• Exposure
• 2 - 14 days after exposure - Symptoms appear
• 2 - 8 weeks after symptoms appear - Death

• Left drag mouse over area to zoom to that area; right click to zoom back to full
• The lines converge on early report with the green line being drawn last. Where there is only a green and purple line, the green line represents the actual excess deaths. Where the lines diverge, the lines have the meanings explained below.
• Blue line is percentage of expected deaths this week as reported by the CDC.
• Red line is the predicted percentage of expected deaths based on reports received from the CDC so far and corrected based on typical reporting delay.
• Green line is the predicted maximum percentage of expected deaths based on reports received from the CDC so far and corrected based on the maximum reporting delay (early reports are low percentage of final value). Because of the wide variation between early reports and final values, the green line is limited to 200% to keep the graph at a reasonable scale.
• Orange line is the predicted minimum percentage of expected deaths based on reports received from the CDC so far and corrected based on the minimum reporting delay (early reports are high percentage of final value).
• Purple line is the accumulated percentage of expected deaths based on data received from the CDC so far.

To Date Summary

The table below shows the actual number of reported deaths since 1/1/20, the expected nmber of deaths, and the excess number of deaths. As discussed above, the expected number is based on the same period for the years 2017 through 2019.

Predictions Based On Early Reports

As discussed above, it takes several weeks for the CDC to receive all the death reports for a specific week. In an attempt to get more current data, a "correction factor" has been developed based on how the percent expected deaths increases after the week of death as more reports are received. Data on report delays has been gathered from June 15, 2020 through May 29, 2021. This data is here. The summary data used for the predictions is here. The "Average Percent of Max" (not really shown as percent; 1.00 = 100%) is the portion of the final value that shows up the specified number of days after the end of the week of the death. The "final value" is the maximum value over time for that weeek as additional reports arrive at the CDC. The reported CDC percent of expected deaths is divided by the Average Percent of Max for the number of days between the end of the week of death and the CDC update date to yield the predicted percent of expected deaths. Based on this data, a predicted percentage of expected deaths is determined immediately following the week of death. As the CDC updates their numbers (every weekday), the correction factors are updated and the predicted percentage of expected deaths is updated. Along with a prediction based on the average correction factor, predictions are made based on the minimum and maximum prediction factors. These are the minimum percentage of final value the specified number of days after the end of week of the reported deaths and the maximum percentage of final value. Data is included in the prediction factor calculations once the percentage of expected deaths as reported by the CDC is unchanged for a week (making it appear this close to the final value). NOTE that the predicated values depend upon consistent reporting rates. If data to the CDC arrives faster than it has in the past, the predicted values will be higher. A graph of the reporting delay is below.

Average Age at Time of Death

The CDC does not publish data revealing the average age at death each week. They do, however, make data available showing the total number of deaths in approximate 10 year age groups each week. This data is here (CSV).

In the graph below, this data is used to compute an average age at death for each week. Records are used where the following conditions are satisfied:

• state is United States
• sex is All Sex

At first, I was expecting the age at death to decrease due to covid-19. We could then say covid-19 has resulted in so many years loss of life. However, it appears that covid-19 has, instead, just upset the balance in the number of deaths between different age groups. It has caused more older people to die causing the average age at time of death to increase. When percentage of expected deaths peaked in April 2020, the average age at death also peaked. When the percentage of expected deaths decreased in June 2020, fewer elderly were dying, so the average age at death also decreased. Then, as the percentage of expected deaths increased in July 2020, the average age at death also increased.

It's interesting to compare this with other data. For example, the life expectancy for someone born today in the US is about 78.539 years (as of 2018). However, people dying today were not born today, so today's life expectancy is not appropriate. We might look at the median age of the US population (38.2 years according to Wikipedia. We could then look at the life expectancy for those born in 1982. The life expectancy chart shows a life expectancy of 74.361 years for those born in 1982. That is still higher than the average age at death shown in the graph above. Looking at the graph above, we are seeing people die at about age 73. Thus they were born around 1947. Life expectancy for those born in 1950 is about 68.2 years according to this CDC document. The current 73 years is between the expected 68.2 years and the expected 74.361 years. As mentioned before, there are likely to be seasonal effects, but there is a fairly dramatic variation in age at death.

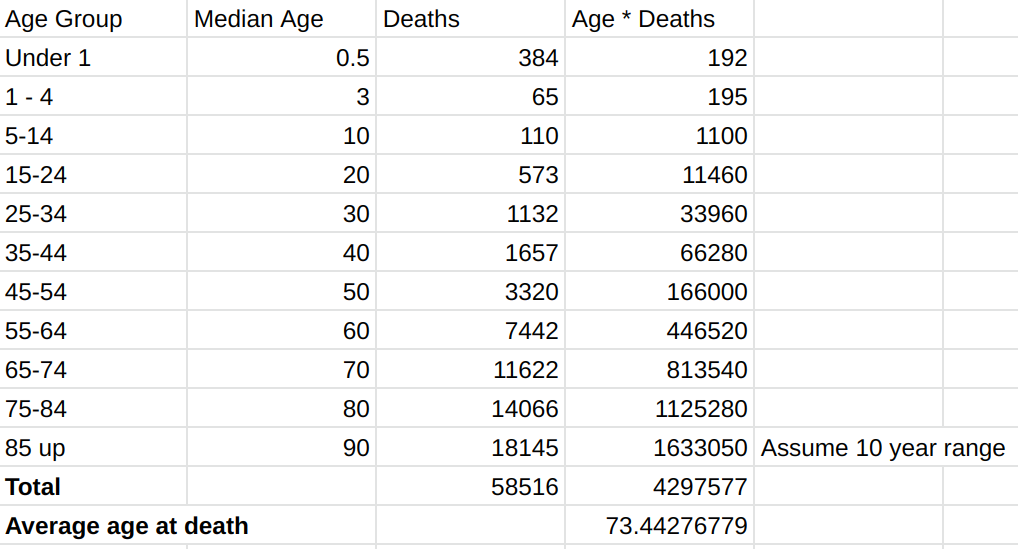
The image below demonstrates the average age at death calculation for February 1, 2020. It can be used to verify the average age at death calculations used to create the graph. The below calculation was done several months ago, and since then more data has shown up. This results in a slight difference between the below calculation and the data in the above graph. The graph above always uses the latest data.

Other Resources

• CDC Wastewater Surveillance - Concentration of Covid virus and 15 day change in concentration in wastewater samples on a plant by plant basis. Provides a good random sampling of Covid in a community.
• CDC Community Level - Check covid risk levels in US counties to determine what precautions, such as mask wearing, to use.
• CDC Coronavirus (COVID-19) - Extensive resources.
• CDC Provisional Death Counts for Coronavirus Disease 2019 (COVID-19) - Daily updates of deaths involving coronavirus disease 2019 (COVID-19), pneumonia, and influenza reported to NCHS by week ending date and by state. This is the source of the data used on this page. Note that the deaths in a week are the deaths that actually occurred in that week, and it takes time for those reports to arrive at the CDC. This is different from data from the New York Times, below, where the date shown is the date the death is reported as opposed to the date it occurred.
• Excess Deaths Associated with COVID-19 - Extensive analysis by the CDC. Shows actual detah counts compared with expected for each week. You can see the seasonal effects clearly. The page also includes an extensive explanation of the analysis techniques including predictions of the number of deaths in a particular week based on early reports.
• Colorado Outbreak Data
• New York Times Covid in the U.S.: Latest Map and Case Count - Updated daily with case count, death count, and geographic data. Note that the chart "New reported deaths by day in the United States" is based on the date of the report, not the date of the death, as used in the CDC data shown above. This causes dramatic drops in the reported deaths on weekends. There are deaths on weekends, but they are often reported later in the week. Also, as shown above, there can be a substantial delay between the date of death and the report reaching the CDC.
• ‘Excess Deaths’ in 2020 Surpassed Those of 1918 Flu Pandemic - Extensive analysis in the New York Times
• U.S. .excess deaths. during pandemic surpassed 1 million, with covid killing most but other diseases adding to the toll, CDC says, Washington Post, 2/15/2022
• Coronavirus disease (COVID-19) pandemic - Extensive resources.

Raw CDC Data

CDC Data as of 04/24/2025

Comments to harold@hallikainen.org